ÇOXMEYARLI TƏHLİLİN QEYRİ-SƏLİS METODLARINDAN İSTİFADƏ ETMƏKLƏ UNİVERSİTET MÜƏLLİMLƏRİNİN FƏALİYYƏT KEYFİYYƏTİNİN KOMPLEKS QİYMƏTLƏNDİRİLMƏSİ

Tədris prosesinin təhlili göstərir ki, bir çox ali məktəblərdə professor-müəllim heyətinin fəaliyyətinin qiymətləndirilməsi sistemli şəkildə aparılmır. Bu, müəllimlərin, ümumiyyətlə, qiymətləndirildiyini inkar etmir: kafedrada vakant müəllim yerlərinin tutulması prosedurundan keçmək qiymətləndirməsiz mümkün deyil. Bununla belə, müəllimlərin fəaliyyətinin sistematik qiymətləndirilməsinin olmamasından danışarkən, bu işin heç bir aydın şəkildə ifadə edilmiş konsepsiyaya əsaslanmamasını nəzərdə tuturuq. Bir sıra universitetlər müəllimlərin fəaliyyət keyfiyyətinin qiymətləndirilməsi üçün müxtəlif üsullar hazırlayıb sınaqdan keçirsə də, ölkəmizdə ümumi qəbul edilmiş metodika hələ də mövcud deyil. Məqalədə 13 göstərici üzrə universitet müəllimlərinin çoxşaxəli fəaliyyətini xarakterizə edən müvafiq məlumatların ekspert və qeyri-səlis təhlilinə əsaslanan hərtərəfli qiymətləndirmə üsulları təklif olunur. 

GİRİŞ

Müəllim fəaliyyətinin keyfiyyətinə nəzarət universitetlərdə təhsil biznes prosesinin ümumi idarə edilməsinin vacib komponentlərindən biridir. Müəllimin akademik fəaliyyəti çoxşaxəlidir. Buraya tədris, tədris-metodiki, elmi-tədqiqat, təşkilati-metodiki və tərbiyə işləri daxildir ki, bunlar, bir qayda olaraq, planlaşdırılmış attestasiya zamanı universitet rəhbərliyi tərəfindən qiymətləndirilir. Bununla belə, operativ idarəetmə nöqteyi-nəzərindən tədris prosesinin daimi monitorinqi və müəllimlərin fəaliyyətinin mütəmadi olaraq çoxmeyarlı qiymətləndirilməsinin aparılması universitet rəhbərliyinin akademik qərarların qəbul etməsinə informasiya-analitik dəstək verə bilər.

Müəllimlərin əməyinin keyfiyyətinin kompleks qiymətləndirilməsi dedikdə, cari problemlərin həlli üçün universitetin akademik resurslarının qiymətləndirilməsi üzrə bir-biri ilə əlaqəli prosedurlar, üsullar və vasitələrin məcmusu başa düşülür. Seçilmiş metodologiyadan asılı olaraq, müəllimlərin çoxşaxəli fəaliyyətinin kompleks qiymətləndirilməsi üçün məlumat mənbələri sənədlər, sorğular, testlər, hesabatlar, müsahibələr, müzakirələrin nəticələri və işgüzar oyunlar ola bilər. Bəzi universitetlərdə qiymətləndirmənin subyektləri (qiymətləndiricilər), əslində, tələbələrin özləridir. Onlar təhsil müddətində tez-tez qarşılaşdıqları və təhsil illərində bir çox məsələlərdə mühüm rol oynayan müəllimləri qiymətləndirmək vərdişlərinə çox tez yiyələnirlər. Lakin tələbələrin qiymətləndirilməsi yalnız tədris fənlərinin keyfiyyətini və müəllimin tədris bacarığını üzə çıxarır. Odur ki, təhsilverənlərin çoxşaxəli fəaliyyətinin inteqral qiymətləndirilməsini formalaşdırmaq üçün subyekt funksiyası HR-departamentə (İnsan Resurları Departamentinə) həvalə edilməlidir. Bu departament universitet rəhbərliyi və ekspert şurası ilə sıx əməkdaşlıq edərək universitetin akademik heyətinin idarə edilməsi üzrə ixtisaslaşdırılmış funksiyaları yerinə yetirir, başqa sözlə desək, HR menecmenti (insan resurslarının idarə edilməsini) həyata keçirir.

Məqalədə təklif olunan metodologiyanın əsas ideyası ekspert heyəti arasında aparılan sorğunun nəticələrini emal etmək üçün qeyri-səlis çoxmeyarlı analiz metodlarından istifadə etməkdir.

MƏSƏLƏNİN QOYULUŞU

[1, 2]-də universitet müəllimlərinin fəaliyyətinin inteqral qiymətləndirilməsi üçün Tennessi Texnoloji Universitetində (ABŞ) aşağıdakı göstəricilər üzrə hazırlanmış meyarlar sistemindən istifadə edilir: x₁ – pedaqoji effektivlik; x₂ – elmi tədqiqat işi; x₃ – xaricdən maliyyələşdirilən tədqiqatlarda iştirak; x₄ – tədqiqat layihələri və fənn tədqiqatları üzrə texniki hesabatlar; x₅ – nüfuzlu orqanlarda iştirak; x₆ – elmi fəaliyyətlə bağlı olmayan ictimai təşkilatlarda təmsilçilik və çıxış; x₇ – dövlət və dövlət siyasətinə təsir göstərən orqanlarda təmsilçilik; x₈ – bələdiyyə, dövlət və məşvərət orqanlarında, müxtəlif komitələrdə xidmət; x₉ – elmi nəşrlərdə əsərlərə istinad; x₁₀ – komitələrdə, komissiyalarda və işçi qruplarında iş; x₁₁ – cari texnoloji məsələlər üzrə konsaltinq; x₁₂ – istehsalla, işəgötürənlərlə birbaşa əlaqə; x₁₃ – texnoloji lisenziyalaşdırma, sertifikatlaşdırma, patentlər.

Korporativ daxili rəqabət amili kimi [1, 2]-də çəkili toplama düsturu ilə hesablanmış universitet müəlliminin akademik göstəricisindən istifadə edilməsi təklif olunur. 

burada α_i – x_i (i = 1÷13) qiymətləndirmə əlamətinin xüsusi çəkisi; e_i – müəllimin akademik və digər fəaliyyətlərinin on ballıq şkala üzrə konsolidasiya edilmiş ekspert qiymətləndirilməsidir. Bu zaman indeks nə qədər yüksək olsa, müəllim çoxşaxəli fəaliyyətinin təhlilinin nəticələrinə əsasən bir o qədər uğurlu hesab olunur.

İlkin məlumat kimi universitet müəllimlərinin fəaliyyəti ilə bağlı ekspert qiymətləndirmələrindən onların x_i (i = 1÷13) qiymətləndirmə əlamətlərinə uyğunluğu üçün istifadə olunur. On ballıq şkala üzrə unifikasiya edildikdən sonra ekspert qiymətləndirmələri hər bir müəllim və hər bir meyar üzrə ortalanır və sistemləşdirilir. Beş müəllim üçün belə məlumatın fraqmenti a_k (k = 1÷5) cədvəl 1-də göstərilir. Bu cədvəldə həm də [1, 2]-də müəyyən edilmiş qiymətləndirmə əlamətlərinin çəkiləri və (1) düsturu ilə hesablanmış uyğun akademik indekslər verilir.

Cədvəl 1. Müəllimlərin universitetdə akademik fəaliyyətini xarakterizə edən ədədi məlumatlar.

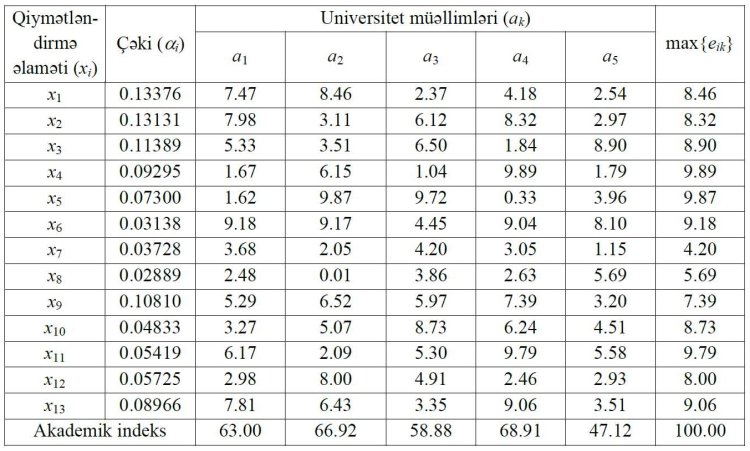
[1, 2]-də verilmiş x_i (i = 1÷13) qiymətləndirmə əlamətlərinə edilmiş şərh və izahlara görə, onlara qeyri-səlis çoxluqlar vasitəsilə ən yaxşı şəkildə təsvir edilən keyfiyyətli və ya zəif strukturlaşdırılmış kateqoriyalar kimi baxılmalıdır. Bu məqsədlə a_k (k = 1÷5) müəllimlərini alternativlər kimi götürərək, universum kimi A = {a₁, a₂, a₃, a₄, a₅} toplusunu seçək. Biz A universumunun qeyri-səlis alt çoxluqları üçün mənsubiyyət funksiyası olaraq Qauss tipli funksiyanı seçirik, yəni

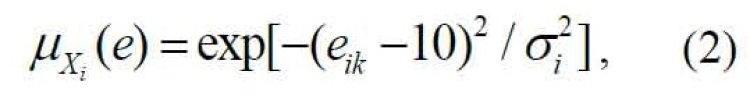
burada e_ik i-ci qiymətləndirmə əlamətinə münasibətdə k-ci müəllimin məmnunluğunun ortalanmış ekspert qiymətləndirməsidir ki, bu qiymətləndirmə müəllimə mövcud olmadığı səviyyəyə uyğunluğuna görə beş ballıq şkala ilə verilir; δ_i = 5 – bütün qeyri-səlislik (fazifikasiya) halları üçün eyni seçilmiş standart kənarlaşmadır.

Şəkil 1. Qauss tipli mənsubiyyət funksiyası

Beləliklə, x_i (i = 1÷13) göstəricilərini linqvistik dəyişənlər kimi götürsək, onların qiymətlərindən birini, yəni diskret A universumu əsasında “KİFAYƏT” terminini müvafiq qeyri-səlis X_i çoxluqları şəklində aşağıdakı qaydada əks etdirə bilərik:

• X₁ = {0.7741/a₁, 0.9095/a₂, 0.0974/a₃, 0.2580/a₄, 0.1080/a₅};
• X₂ = {0.8494/a₁, 0.1497/a₂, 0.5476/a₃, 0.8932/a₄, 0.1385/a₅};
• X₃ = {0.4180/a₁, 0.1855/a₂, 0.6126/a₃, 0.0697/a₄, 0.9528/a₅};
• X₄ = {0.0623/a₁, 0.5527/a₂, 0.0403/a₃, 0.9995/a₄, 0.0675/a₅};
• X₅ = {0.0603/a₁, 0.9993/a₂, 0.9969/a₃, 0.0237/a₄, 0.2324/a₅};
  
• X₆ = {0.9735/a₁, 0.9728/a₂, 0.2917/a₃, 0.9638/a₄, 0.8655/a₅};
  
• X₇ = {0.2024/a₁, 0.0798/a₂, 0.2604/a₃, 0.1448/a₄, 0.0436/a₅};
  
• X₈ = {0.1041/a₁, 0.0185/a₂, 0.2214/a₃, 0.1139/a₄, 0.4757/a₅};
  
• X₉ = {0.4117/a₁, 0.6161/a₂, 0.5222/a₃, 0.7615/a₄, 0.1573/a₅};
  
• X₁₀ = {0.1634/a₁, 0.3783/a₂, 0.9375/a₃, 0.5681/a₄, 0.2995/a₅};
  
• X₁₁ = {0.5561/a₁, 0.0819/a₂, 0.4133/a₃, 0.9982/a₄, 0.4577/a₅};
  
• X₁₂ = {0.1393/a₁, 0.8521/a₂, 0.3548/a₃, 0.1029/a₄, 0.1354/a₅};
  
• X₁₃ = {0.8254/a₁, 0.6006/a₂, 0.1705/a₃, 0.9653/a₄, 0.1855/a₅}.

x_i (i = 1÷13) göstəricilərinə uyğun olaraq müəllimin fəaliyyətindən məmnunluğun qiymətləndirilməsi üçün əsas əlamət kimi “KİFAYƏTDİR” terminini təsvir edən qeyri-səlis formalizmlərdən istifadə edərək, uyğun gələn qeyri-səlis çoxmeyarlı qiymətləndirmə metodlarını adaptasiya etmək lazımdır.

QEYRİ-SƏLİS ÇIXARIŞ ÜSULU İLƏ MÜƏLLİMLƏRİN AKADEMİK FƏALİYYƏTİNİN QİYMƏTLƏNDİRİLMƏSİ

Universitetdə müəllimlərin fəaliyyətinin keyfiyyətinin qiymətləndirilməsi üçün x_i (i = 1÷13) qiymətləndirmə meyarları nəzərə alınmaqla aşağıdakı ardıcıl mülahizələr əsas götürülüb:

d₁: Əgər pedaqoji səmərəlilik və elmi-tədqiqat işləri, elmi-tədqiqat layihələri və sahə araşdırmaları üzrə texniki hesabatlar, nüfuzlu orqanlarda iştirak, komitələrdə, komissiyalarda və işçi qruplarında işi, istehsalçılarla (işəgötürənlərlə) birbaşa əlaqə, texnoloji lisenziyalaşdırma və patent üzrə sertifikatlaşma kifayətdirsə, onda müəllimin fəaliyyəti qənaətbəxşdir;

d₂: Pedaqoji səmərəlilik və elmi tədqiqat işi, elmi-tədqiqat layihələri və sahə araşdırmaları üzrə texniki hesabatlar, nüfuzlu orqanlarda iştirak, elmi fəaliyyətlə bağlı olmayan ictimai təşkilatlarda təmsilçilik və çıxışlar kifayətdirsə, ictimai və dövlət siyasətinə təsir göstərən orqanlarda təmsilçilik yetərincədirsə, bələdiyyə, dövlət və məşvərət orqanlarında, müxtəlif komitələrdə xidmət, komitələrdə, komissiyalarda və işçi qruplarda iş, cari texnoloji məsələlər üzrə məsləhətləşmələr lazım olan səviyyədədirsə, istehsalçılarla (işəgötürənlərlə) birbaşa əlaqə, texnoloji lisenziyalaşdırma və patent üzrə sertifikatlaşma kifayətdirsə, onda müəllimin fəaliyyəti qənaətbəxşdən də yuxarıdır;

d₃: Tədris səmərəliliyi və elmi-tədqiqat işi, xaricdən maliyyələşdirilən tədqiqatlarda iştirak, elmi-tədqiqat layihələri və intizam tədqiqatları üzrə texniki hesabatlar, nümayəndəlik orqanlarında iştirak, elmi fəaliyyətlə bağlı olmayan ictimai təşkilatlarda təmsilçilik və çıxış, fəaliyyət, dövlət və dövlət siyasətinə təsir göstərən orqanlarda təmsilçilik, bələdiyyə, dövlət və məşvərət orqanlarında, müxtəlif komitələrdə xidmət, elmi nəşrlərdə əsərlərə istinad, komitə, komissiya və işçi qruplarında iş, cari texnoloji məsələlər üzrə məsləhət xidmətləri, istehsalatla (işəgötürənlərlə) birbaşa əlaqə, texnoloji lisenziyalaşdırma və patentlərlə sertifikatlaşma kifayət səviyyədədirsə, onda müəllimin fəaliyyəti qüsursuzdur;

d₄: Pedaqoji səmərəlilik və elmi-tədqiqat işləri, xaricdən maliyyələşdirilən tədqiqatlarda iştirak, elmi-tədqiqat layihələri və sahə araşdırmaları üzrə texniki hesabatlar, nüfuzlu orqanlarda iştirak, elmi nəşrlərdə əsərlərə istinadlar, komitələrdə, komissiyalarda və işçi qruplarda fəaliyyət, cari texnoloji məsələlər üzrə məsləhət xidmətləri, istehsalatla (işəgötürənlərlə) birbaşa əlaqə, texnoloji lisenziyalaşdırma və patentlərlə sertifikatlaşma kifayət səviyyədədirsə, onda müəllimin fəaliyyəti qüsursuzdur;

d₅: Pedaqoji səmərəlilik və tədqiqat işi, xaricdən maliyyələşdirilən tədqiqatlarda iştirak, elmi-tədqiqat layihələri və sahə tədqiqatları üzrə texniki hesabatlar, nüfuzlu orqanlarda iştirak kifayətdirsə, elmi fəaliyyətlə bağlı olmayan ictimai təşkilatlarda təmsilçilik və çıxışlar kifayət deyilsə, ictimai və dövlət siyasətinə təsir göstərən orqanlarda təmsilçilik, komitələrdə, komissiyalarda və işçi qruplarda iş kifayət qədərdirsə, cari texnoloji məsələlər üzrə məsləhətləşmələr kifayət qədər səviyyədədir, istehsalatla (işəgötürənlərlə) birbaşa əlaqə kifayət deyildirsə, texnoloji lisenziyalaşma və patentlərlə sertifikatlaşma kifayətdirsə, onda müəllimin fəaliyyəti də qənaətbəxşdir;

d₆: Pedaqoji səmərəlilik və elmi-tədqiqat işləri, elmi-tədqiqat layihələri və sahə tədqiqatları üzrə texniki hesabatlar, elmi nəşrlərdə əsərə istinadlar kifayət qədər deyilsə, onda müəllimin fəaliyyəti qeyri-qənaətbəxşdir.

Göstərilən ekspert mülahizələrini əsas verbal model kimi qəbul etmək olar; bu modeldə giriş xüsusiyyətləri “KİFAYƏTDİR” ümumi adı altında qiymətləndirici xüsusiyyətlərdir, çıxış xarakteristikaları isə “QEYRİ-QƏNAƏTBƏXŞ”, “QƏNAƏTBƏXŞ”, “DAHA QƏNAƏTBƏXŞ” linqvistik terminlərdir. “ÇOX QƏNAƏTBƏXŞ”, “MÜKƏMMƏL”. Bu modelin qeyri-səlis mühitdə realizasiyasını X_i (i = 1÷13) qeyri-səlis çoxluqları şəklində əvvəlcədən müəyyən edilmiş girişləri olan müvafiq qeyri-səlis çıxarış sistemi təmin edilə bilər. Bu sistemin çıxışlarının qeyri-səlis təsviri üçün U = {0, 0.1, 0.2, …, 0.9, 1} diskret çoxluğu universum kimi seçilir. Bu halda [3]-ə uyğun olaraq ∀_u ∈ U üçün aşağıdakıları alırıq:

• S = SATISFACTORY: μ_S(u) = u;
• MS = MORE THAN SATISFACTORY: μ_MS (u) = √u;
• VS = VERY SATISFACTORY: μ_VS(u) = u²;
• P = PERFECT:
• US = UNSATISFACTORY: μ_US(u) = 1–u.

Nəticədə, d₁ ÷ d₆ mülahizələrini simvolik formada aşağıdakı kimi görünən implikativ qaydalar kimi başqa şəkildə ifadə etmək olar:
d₁: (x₁ = X₁) & (x₂ = X₂) & (x₄ = X₄) & (x₅ = X₅) & (x₁₀ = X₁₀) & (x₁₂ = X₁₂) & (x₁₃ = X₁₃) ⇒ (y = S);
d₂: (x₁ = X₁) & (x₂ = X₂) & (x₄ = X₄) & (x₅ = X₅) & (x₆ = X₆) & (x₇ = X₇) & (x₈ = X₈) & (x₁₀ = X₁₀) & (x₁₁ = X₁₁) &(x₁₂ = X₁₂) & (x₁₃ = X₁₃) ⇒ (y = MS);
d₃: (x₁ = X₁) & (x₂ = X₂) & (x₃ = X₃) & (x₄ = X₄) & (x₅ = X₅) & (x₆ = X₆) & (x₇ = X₇) & (x₈ = X₈) & (x₉ = X₉) & (x₁₀ = X₁₀) & (x₁₁ = X₁₁) &(x₁₂ = X₁₂) &(x₁₃ = X₁₃) ⇒ (y = P);
d₄: (x₁ = X₁) & (x₂ = X₂) & (x₃ = X₃) & (x₄ = X₄) & (x₅ = X₅) & (x₉ = X₉) & (x₁₀ = X₁₀) & (x₁₁ = X₁₁) & (x₁₂ = X₁₂) &(x₁₃ = X₁₃) ⇒ (y = VS);
d₅: (x₁ = X₁) & (x₂ = X₂) & (x₃ = X₃) & (x₄ = X₄) & (x₅ = X₅) & (x₆ = -X₆) & (x₇ = -X₇) & (x₁₀ = X₁₀) & (x₁₁ = X₁₁) &(x₁₂ = -X₁₂) & (x₁₃ = X₁₃) ⇒ (y = S);
d₆: (x₁ = -X₁) & (x₂ = -X₂) & (x₄ = -X₄) & (x₉ = -X₉) ⇒ (y = US).

İmplikativ qaydaların [4] sol tərəflərindən qeyri-səlis çoxluqlarla kəsişmə əməliyyatını tətbiq edərək və Lukaseviçin məlum implikasiyasından μ(a, u) = min{1, 1-μ(a)+μ(u)} istifadə edərək, müvafiq matrislər şəklində qeyri-səlis münasibətlər əldə edirik. Bunlar aşağıdakılardır:

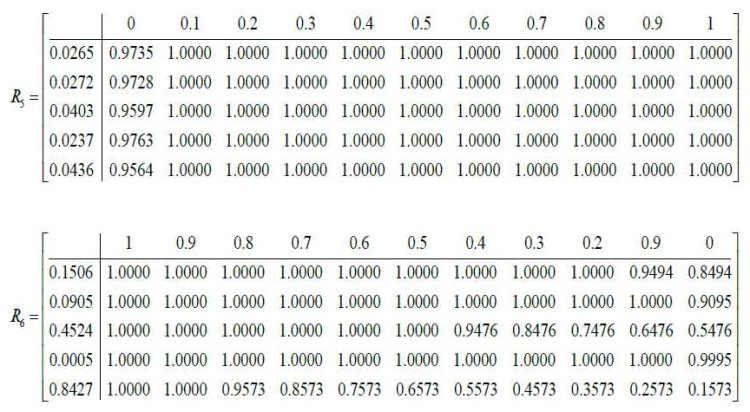
“MIN” əməliyyatından istifadə etməklə bu matrislərin kəsişməsi R₁ ∩ R₂ ∩ ... ∩ R₆ son nəticədə vahid R matrisi şəklində ümumi funksional həlli verir. [3]-ə əsasən müəllimin fəaliyyətinin qənaətbəxş olmasının qiymətləndirilməsi ilə bağlı qeyri-səlis nəticə məmnunluq R (k = 1÷5) matrisinin k-cı sətrindən mənsubiyyət funksiyasının müvafiq qiymətləri ilə U universiumunun qeyri-səlis E_j alt çoxluğu şəklində əks olunur:

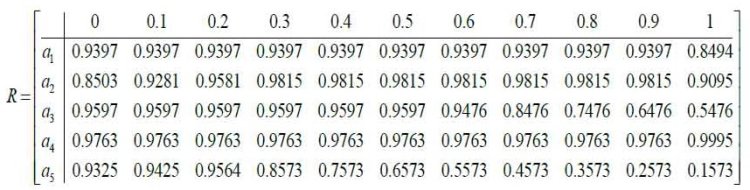
Qeyd olunmuş a_k (k = 1÷5) müəllimlərinin fəaliyyətindən məmnunluqla bağlı qeyri-səlis nəticələrin ədədi qiymətləndirilməsi üçün qeyri-səlisləşdirmə (defazifikasiya) prosedurundan istifadə olunur. Beləliklə, qeyri-səlis çoxluq şəklində əks olunan a₅ müəlliminin fəaliyyətindən məmnunluqla bağlı qeyri-səlis nəticə üçün (R matrisinin 5-ci sətrinə baxın).

E₅ = {0.9325/0, 0.9425/0.1, 9664/0.2, 0.8573/0.3, 0.7573/0.4, 0.6573/0.5, 0.5573/0.6, 0.4573/0.7, 0.3573/0.8, 0.2573/0.9, 0.1573/1}, α-səviyyəli E_5α çoxluqlarını quraraq və

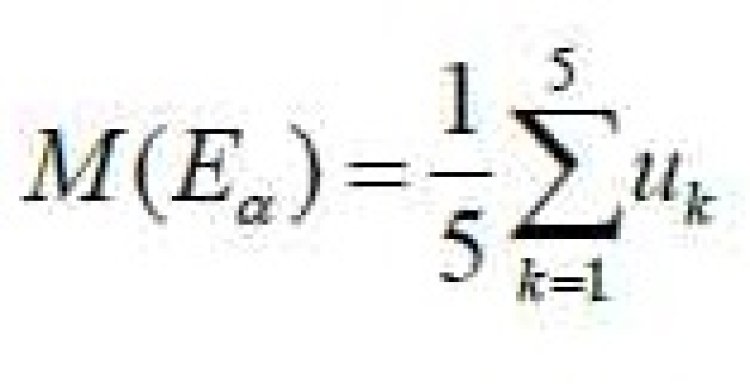
düsturu üzrə onlara uyğun olan çoxluq güclərini hesablayaraq alırıq:

• for 0<α<0.1573: Δα = 0.1573, E_5α = {0, 0.1, 0.2, 0.3, …, 0.8, 0.9, 1}, M(E_5α) = 0.50;
• for 0.1573<α<0.2573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3, …, 0.8, 0.9}, M(E_5α) = 0.45;
• for 0.2573<α<0.3573: Δα = 0.1, E_5α={0, 0.1, 0.2, 0.3, …, 0.7, 0.8}, M(E_5α) = 0.40;
• for 0.3573<α<0.4573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3, …, 0.6, 0.7}, M(E_5α) = 0.35;
• for 0.4573<α<0.5573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6}, M(E_5α) = 0.30;
• for 0.5573<α<0.6573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3, 0.4, 0.5}, M(E_5α) = 0.25;
• for 0.6573<α<0.7573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3, 0.4}, M(E_5α) = 0.20;
• for 0.7573<α<0.8573: Δα = 0.1, E_5α = {0, 0.1, 0.2, 0.3}, M(E_5α) = 0.15;
• for 0.8573<α<0.9325: Δα = 0.0752, E_5α = {0, 0.1, 0.2}, M(E_5α) = 0.10;
• for 0.9325<α<0.9425: Δα = 0.01, E_5α = {0.1, 0.2}, M(E_5α) = 0.15;
• for 0.9425<α<0.9564: Δα = 0.0139, E_5α = {0.2}, M(E_5α) = 0.20;

[3]-ə görə a5 müəlliminin fəaliyyətindən məmnunluqla bağlı qeyri-səlis çıxarışın ədədi qiymətləndirilməsi (defazifikasiysı) aşağıdakı düstur üzrə hesablanır:

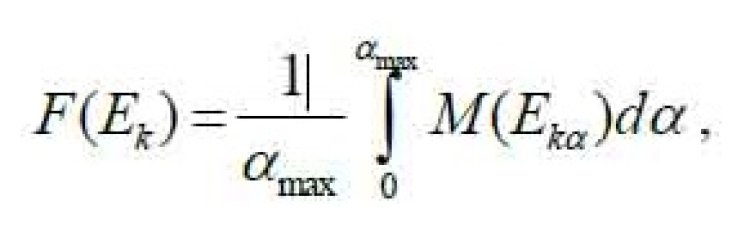
a₅ -ə münasibətdə qeyri-səlis çıxarış üçün alırıq:

Analoji şəkildə digər müəllimlər üçün onların fəaliyyətindən məmnunluğundan qeyri-səlis çıxarışların ədədi qiymətləndirilməsi həyata keçirilir: a₁ → 0.4952; a₂ → 0.5069; a₃ → 0.4448; a₄ → 0.5116. Ən yüksək qeyri-səlisləşdirilmə qiymətinə uyğun olan universitet müəllimi akademik fəaliyyətin keyfiyyəti baxımından ən yaxşısı hesab olunur. Hesablamalardan göründüyü kimi, bu a₄ müəllimidir. Bunun ardınca, defazifikasiya olunmuş qiymətlərin azalma ardıcıllığı ilə a₂, a₁, a₃ və a₅ müəllimləri gəlir.

QEYRİ-SƏLİS MAXMİN KONVOLYUSİYA METODUNDAN İSTİFADƏ EDƏRƏK MÜƏLLİMLƏRİN AKADEMİK FƏALİYYƏTİNİN QİYMƏTLƏNDİRİLMƏSİ

Universitet müəllimlərinin akademik fəaliyyətinin çoxmeyarlı qiymətləndirilməsi üçün qeyri-səlis maxmin konvolyusiya metodundan istifadə olunması optimal alternativlər çoxluğunun qurulmasını nəzərdə tutur [3]. Həll olunan problem kontekstində bu prosedur “KİFAYƏTDİR” qiymətləndirmə əlamətinə (meyarına) uyğun olaraq müəllimlərin akademik fəaliyyətinin ekspert qiymətləndirmələrini əks etdirən X_i (i = 1÷13) qeyri-səlis çoxluqlarının kəsişməsinin tapılması yolu ilə həyata keçirilir:

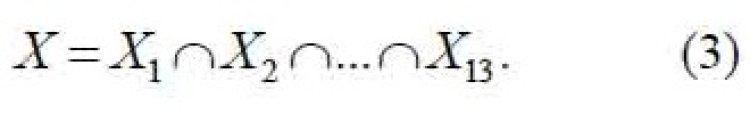
Maxmin konvolyusiya metoduna görə, akademik fəaliyyət baxımından ən uğurlu olan, mənsubluq funksiyasının ən yüksək qiymətinə  malik olan müəllim a*dur:

[4]-ə əsasən qeyri-səlis çoxluqların kəsişməsi əməliyyatı a_k (k = 1÷5) alternativi üçün minimum qiymətin seçilməsinə uyğundur:

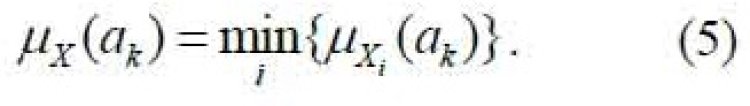
Bizim halda optimal alternativlər çoxluğu (4) və (5)-dən istifadə edərək aşağıdakı kimi qurulur:
X = {min{0.7741, 0.8494, 0.4180, 0.0623, 0.0603, 0.9735, 0.2024, 0.1041, 0.4117, 0.1634, 0.5561, 0.1393, 0.8254}; min{0.9095, 0.1497, 0.1855, 0.5527, 0.9993, 0.9728, 0.0798, 0.0185, 0.6161, 0.3783, 0.0819, 0.8521, 0.6006}; min{0.0974, 0.5476, 0.6126, 0.0403, 0.9969, 0.2917, 0.2604, 0.2214, 0.5222, 0.9375, 0.4133, 0.3548, 0.1705}; min{0.2580, 0.8932, 0.0697, 0.9995, 0.0237, 0.9638, 0.1448, 0.1139, 0.7615, 0.5681, 0.9982, 0.1029, 0.9653}; min{0.1080, 0.1385, 0.9528, 0.0675, 0.2324, 0.8655, 0.0436, 0.4757, 0.1573, 0.2995, 0.4577, 0.1354, 0.1855}}.

Bu halda akademik fəaliyyətin keyfiyyəti ilə bağlı alternativ ekspert qərarları üçün prioritetlərin nəticə vektoru aşağıdakı formaya malik olur:

max {μX(ak)} = max {0.0603, 0.0185, 0.0403, 0.0237, 0.0436}.

Akademik fəaliyyətin keyfiyyətinin qiymətləndirilməsi nöqteyi-nəzərindən ən yaxşı müəllim a₁ olur, belə ki, (5)-ə görə ona 0.0603 maksimum komponenti uyğundur. Qalan müəllimlər uyğun qiymətlərin azalma ardıcıllığı ilə sıralanır: a₅ → 0.0436; a₃ → 0.0403; a₄ → 0.0237; a₂ → 0.0185.

Son düzülüşdən göründüyü kimi, o əvvəlkindən xeyli dərəcədə fərqlənir. Bu onunla izah olunur ki, X_i (i = 1÷13) qiymətləndirmə əlamətləri müxtəlif dərəcələrdə əhəmiyyət kəsb edir. Buna görə də, onların optimal alternativlər çoxluğunun qurulmasına xüsusi töhfəsi çəkili kəsişmə şəklində əks olunmalıdır.

burada α₁ = 0.13376, α₂ = 0.13131, α₃ = 0.11389, α₄ = 0.09295, α₅ = 0.07300, α₆ = 0.03138, α₇ = 0.03728, α₈ = 0.02889, α₉ = 0.10810, α₁₀ = 0.04833, α₁₁ = 0.05419, α₁₂ = 0.05725, α₁₃ = 0.08966 – [1, 2]-də nəzərdən keçirilən nümunə üçün müəyyən edilmiş universitet  müəllimlərinin akademik fəaliyyətinin məcmu göstəricisini qiymətləndirmək üçün müvafiq meyarların çəkiləridir.

(6)-nı nəzərə alsaq, alarıq:

X = {min {0.7741^0.13376, 0.8494^0.13131, 0.4180^0.11389, 0.0623^0.09295, 0.0603^0.07300, 0.9735^0.03138, 0.2024^0.03728, 0.1041^0.02889, 0.4117^0.10810, 0.1634^0.04833, 0.5561^0.05419, 0.1393^0.05725, 0.8254^0.08966}; min {0.9095^0.13376, 0.1497^0.13131, 0.1855^0.11389, 0.5527^0.09295, 0.9993^0.07300, 0.9728^0.03138, 0.0798^0.03728, 0.0185^0.02889, 0.6161^0.10810, 0.3783^0.04833, 0.0819^0.05419, 0.8521^0.05725, 0.6006^0.08966}; min {0.0974^0.13376, 0.5476^0.13131, 0.6126^0.11389, 0.0403^0.09295, 0.9969^0.07300, 0.2917^0.03138, 0.2604^0.03728, 0.2214^0.02889, 0.5222^0.10810, 0.9375^0.04833, 0.4133^0.05419, 0.3548^0.05725, 0.1705^0.08966}; min {0.2580^0.13376, 0.8932^0.13131, 0.0697^0.11389, 0.9995^0.09295, 0.0237^0.07300, 0.9638^0.03138, 0.1448^0.03728, 0.1139^0.02889, 0.7615^0.10810, 0.5681^0.04833, 0.9982^0.05419, 0.1029^0.05725, 0.9653^0.08966}; min {0.1080^0.13376, 0.1385^0.13131, 0.9528^0.11389, 0.0675^0.09295, 0.2324^0.07300, 0.8655^0.03138, 0.0436^0.03728, 0.4757^0.02889, 0.1573^0.10810, 0.2995^0.04833, 0.4577^0.05419, 0.1354^0.05725, 0.1855^0.08966}}.

Bu halda tələb olunan vektor belədir: (0.7726, 0.7793, 0.7324, 0.7383, 0.7425), buradan (5)-ə uyğun olaraq akademik fəaliyyətin keyfiyyətinə görə ən yaxşı müəllim a₂ hesab olunur, onun göstəricisi (2-ci komponent) axtarılan vektorun tərkibində ən böyüyüdür (0.7793). Digər müəllimlər müvafiq göstəricilərin azalma ardıcıllığı ilə sıralanır: a₁ → 0.7726, a₅ → 0.7425, a₄ → 0.7383, a₃ → 0.7324.

Beş müəllimin pedaqoji fəaliyyətinin keyfiyyətinin qiymətləndirilməsi üçün müxtəlif üsullarla əldə olunmuş nəticələri Cədvəl 2-də göstərilir.

Cədvəl 2. Müəllimlərin akademik fəaliyyətinin inteqral qiymətləndirilməsinin nəticələri

Baxılan bütün nümunələrdə əsas məlumatların vahid, ardıcıl və ziddiyyətsiz (bax [1, 2]) olmasına baxmayaraq, ümumi çəkili qiymətləndirmə metodundan və qeyri-səlis çıxarış sistemindən istifadə etməklə əldə edilən sıralama nəticələri, qeyri-səlis maxmin konvolyusiya metodlarından istifadə etməklə alınan müvafiq nəticələrdən kəskin şəkildə fərqlənir. Ümumi çəkili qiymətləndirmə metodu və qeyri-səlis çıxarış sistemi mütəxəssislərin intuitiv fikirləri ilə yaxşı uyğunlaşan tamamilə eyni sıralama nəticələrini verdi. Eyni zamanda implikativ qaydalara əsaslanan evristik yanaşmanı həyata keçirən uyğunlaşdırılmış qeyri-səlis çıxarış sistemini ən uğurlu qiymətləndirmə mexanizmi hesab etmək olar.

Müxtəlif üsullarla alınan nəticələr arasındakı uyğunsuzluq, bir tərəfdən, ekspert məlumatlarının müxtəlif təqdim olunma üsulları ilə, digər tərəfdən isə çoxmeyarlı qiymətləndirməyə yanaşmaların müxtəlifliyi ilə izah olunur. Beləliklə, ümumi çəkili qiymətləndirmə və qeyri-səlis çıxarış üsulları rasional balanslaşdırılmış yanaşmaya əsaslanır. Maxmin konvolyusiya, alternativlərin “yaxşı” tərəflərini nəzərə almayan pessimist yanaşmanın həyata keçirilməsidir. Halbuki bütün meyarlar üzrə minimal çatışmazlıqlara malik olan alternativ ən yaxşı hesab olunur. 

NƏTİCƏ

Qeyri-səlis modellərdən istifadə etməklə alternativlərin çoxmeyarlı qiymətləndirilməsi üçün məqalədə istifadə olunan üsullar ayrı-ayrı meyarlar üzrə universitet müəllimlərinin akademik fəaliyyətinin keyfiyyətini rahat və kifayət qədər obyektiv qiymətləndirməyə imkan verir. Klassik qiymətləndirmə metodlarından fərqli olaraq, nəzərdən keçirilən siyahıya yeni müəllimlərin əlavə edilməsi əvvəlki sıralanmış dəstlərin ardıcıllığını dəyişmir. Hətta alternativlər qiymətləndirmə əlamətlərinə (meyarlarına) əsasən qiymətləndirərkən qeyri-səlis yanaşma həm şifahi qiymətləndirməni, həm də meyarların mənsubiyyət funksiyalarından istifadə edərək nöqtəvi qiymətləndirmə əsasında kəmiyyət qiymətləndirməsini təmin edir.

Qeyri-səlis modellərdən istifadə etməklə çoxmeyarlı qiymətləndirmənin əsas problemi meyarlarla inteqral qiymətləndirmə metodları arasında qarşılıqlı əlaqələr haqqında məlumatların təqdim edilməsidir. Bununla belə, cədvəl 2-dən göründüyü kimi, müxtəlif yanaşmalara əsaslanan qeyri-səlis üsullar fərqli nəticələr verir. Hər bir yanaşmanın öz məhdudiyyətləri və xüsusiyyətləri vardır ki, istifadəçi bu və ya digər qərar qəbuletmə metodundan istifadə etməzdən əvvəl onları başa düşməlidir. Məlumatın təqdim edilməsi üçün daha geniş imkanları şifahi modelləşdirməyə əsaslanan və ən stabil olan qeyri-səlis çıxarış sistemi ilə dəstəklənən evristik yanaşma təmin edir.

Universitet müəllimlərinin akademik fəaliyyətinin keyfiyyətinin qiymətləndirilməsində qeyri-səlis metodların tətbiqinin təhlili bu sahədə gələcək tədqiqatlar üçün tələbləri formalaşdırmağa imkan verir. Bunlar, əslində, qiymətləndirmə meyarları arasında mürəkkəb qarşılıqlı əlaqələrin təsvirinə nəzəri yanaşmaların işlənib hazırlanması, qeyri-səlis təsviretmədən istifadə etməklə hibrid modelləşdirmə sistemlərinə əsaslanan intellektual qərarqəbuletmə üsullarından daha geniş istifadə edilməsidir. 

İstifadə edilmiş ədəbiyyat

¹ Mardanov, M.J., Aliyev, E.R., Rzayev, R.R., Abdullayev, Kh.Kh. (2023). Formation of the academic index of a university teacher based on weighted evaluation criteria. The Springer Series “Lecture Notes in Networks and Systems”, 758, Vol. 2, pp. 600-608. 
² Mardanov, M.J., Aliyev, E.R., Rzayev, R.R., Abdullayev, Kh.Kh. (2023). Universitet müəllimlərinin akademik fəaliyyətini əks etdirən göstəricilərinin ekspert təhlili əsasında inteqral indeksinin hesablanması. Azerbaijan Journal of Educational Studies, №2, pp. 10-20 (in Azerbaijani)
³ Andreychikov, A.V., Andreychikova, O.N. (2000). Analiz, sintez, planirovaniye resheniy v ekonomike – Moskva: Finansy i statistika,. 368 s.: il.
⁴ Zadeh, L. (1975). The concept of a linguistic variable and its application to approximate reasoning – I // Information sciences. 8(3). P. 199-249.